DIALOG TENTANG BOLA DAN KOTAK

DIALOG TENTANG BOLA DAN KOTAK

Armahedi Mahzar © 2016

Ketika Ki Algo menunjukkan metoda aksiomatik Spencer-Brown bagi aljabar Boole untuk menurunkan kesimpulan suatu silogisme absah, Ni Suiti senang sekali mendapatkan metoda yang sangat mudah, begitu mudahnya sehingga bisa diperlajari oleh anak-anak SMP.

Namun, setelah mencobanya dan mengamati dengan cermat metoda itu, Ni Suiti pun terilhami untuk mensimulasi metoda pembuktian itu dengan sebuah permainan hapus-hapusan gambar . Ketika dia menerangkan permainan itu, dia menggunakan gambar bola warna-warni dan gambar kotak. Dengarkanlah dialog antara kedua kakek nenek itu.

Ki Algo: Apa sih, metoda TK kamu itu?

Ni Suiti: Ini bukan metoda, tapi sekedar permainan hapus gambar yang ajaib. Permainan ini bisa mensimulasi deduksi suatu silogisme itu benar, bahkan bisa menunjukkan mana silogisme yang salah.

Ki Algo: Permainan TK?

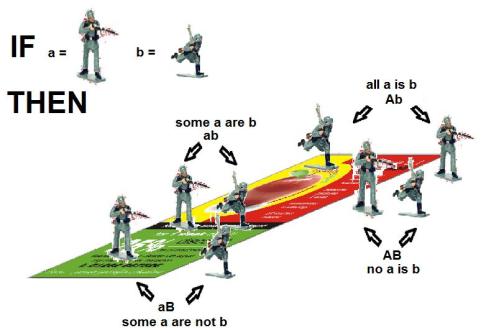
Ni Suiti: Ya, begitulah. Saya akan pakai gambar bola warna-warni dan gambar kotak untuk memainkannya. Tapi tentu saja gambar bola berwarna bisa diganti dengan mainan apa saja yang mempunyai duplikat seperti misalnya gambar tentara timah. Begitu juga kotak bisa diganti dengan gambar sehelai kertas.

Ki Algo: Pakai saja gambar bola dan gambar kotak saja sebagai contoh. Bagaimana kita menyatakan silogisme JIKA p DAN q, MAKA r. Dalam notasi kurung ini dinyatakan dalam rumus [pq[r]].

Ni Suiti:: p, q dan r kita nyatakan gambar-gambar bola merah, bola hijau dan bola biru. Gambar dari silogisme [pq[r]] adalah


di mana p, q dan r adalah gambar-gambar dari pernyataan kategoris Aristoteles.

Ki Algo: Bagaimana kita menggambarkan pernyataan-pernyataan kategoris Aristoteles?

Ni Suiti: Begini saja. Lihat saja susunan bola untuk keempat pernyataan kategoris Aristoteles dalam tabel yang sudah saya bikin ini.

Ki Algo: Bagaimana cara memainkannya?

 

Ni Suiti: Hanya dua tahap, yaitu susun-menyusun alasan dan bongkar-membongkar mencari kesimpulan. Aturan penyusunan sesuai dengan apa yang tertera pada tabel di atas.

Ki Algo: Aturan pembongkarannya?

Ni Suiti: Aturan pembongkaran hanya satu, yaitu buang pasangan bola sewarna yang letaknya berseberangan.

Ki Algo: Berilah contohnya yang kongkret!

Ni Suiti: Inilah silogisme yang dinamai Celarent: KARENA SEMUA b TIDAK c DAN SEMUA a ITU b MAKA SEMUA a TIDAK c. Susunan bola Celarent ada pada bagian kiri gambar di bawah ini

Pembuktian Celarent

Pembuktian dilakukan dengan menghapus gambar dengan 3 aturan penghapusan gambar berikut ini
(1) hapus kotak yang lansung berada dalam kotak yang lebih besar
(2) hapus gambar dalam kotak jika gambar yang sama ada di luar kotak tersebut.
(3) hapus semua gambar yang berada di luar kotak yang kosong.



Dalam pembuktian di atas, kita lakukan aturan (2) dua kali, lalu aturan (3), akhirnya aturan (1)

Ki Algo: Penyimpulan dalam perumusan  saya adalah penghitungan, dalam permainan bola kotak kamu berupa penyederhanaan susunan dengan cara membuang gambar-gambar.

Memang mudah sekali. Bisa diajarkan pada anak TK. Tidak perlu hitung-menghitung. Bagaimana dengan silogisme lain dalam tabel Leibniz.

Ni Suiti: lihat saja tabel gambar berikut ini

Tabel susunan pelambang alasan silogisme absah Leibniz

Lakukan ketiga aturan ini: (1) hapus semua gambar kotak yang langsung dalam kotak, (2) hapus gambar di dalam suatu kotak jika gambar yang sama berada di luar kotak tersebut dan (3) hapus semua gambar yang langsung berada di luar sebuah kotak sehingga akhirnya kita mendapat sebuah kertas kosong.

Ki Algo: Wah, mudah sekali. Saya tidak pernah membayangkan kalau logika bisa diajarkan pada anak TK.

Ni Suiti: Tentu saja kita tidak menyebutkan logika pada mereka. Mereka hanya kita ajak bermain dengan aturan-aturan logika tersamar sebagai aturan permainan susun bongkar. Untung-untung aturan itu tertanam di otak mereka sebagai algoritma deduksi silogisme.

Ki Algo: Bagusnya kamu bikin youtubenya. Mudah-mudahan bisa viral.

Ni Suiti: Insya Allah.

SEPASANG SYAIR LOGIKA

SEPASANG SYAIR LOGIKA

Armahedi Mahzar (c) 2016

SYAIR ARITMETIKA LOGIKA

Ketika Ki Algo menemukan sebuah metoda
di mana TIDAK dilambangkan PLUS SATU MINUS
lalu DAN dilambangkan MINUS SATU PLUS
seperti yang dilakukan George Boole,

sementara pernyataan kategoris Aristoteles
SEMUA anu ITU atau TIDAK begitu
serta SEBAGIAN anu ITU atau TIDAK begitu
semuanya bisa dinyatakan sebagai rumus di mana

SEMUA dilambangkan PLUS SATU MINUS
yang juga merupakan pelambang bagi TIDAK
SEBAGIAN dilambangkan dengan PLUS
yang juga merupakan pelambang bagi ITU,

maka kesimpulan semua silogisme
bisa disimpulkan dengan cara
menggabungkan pelambang kedua alasan
dengan pelambang DAN lalu dihitung

Jika hasil dari perhitungan itu adalah
pelambang pernyataan kategoris
maka silogisme itu pastilah absah
tak mungkin disangkal siapa pun

Contohnya silogisme Barbara
KARENA SEMUA anu ITU begini
DAN SEMUA begini ITU begitu
MAKA SEMUA anu ITU begitu

pelambang bagi gabungan alasannya
adalah +1-anu+begini-1+1-begini+begitu
= +1-anu+begitu yaitu pelambang
bagi kesimpulan SEMUA anu ITU begitu

Begitu pula keduapuluh empat
silogisme absah temuan Leibniz
bisa dibuktikan dengan cara sama:
perumusan aritmetika bagi logika

==========================================

SYAIR POETIKA SILOGISME

Ni Suiti melihat rumus-rumus aritmetika
bagi silogisme yang ditemukan Ki Algo
segera mendapat ilham dalam dunia sastra
mengganti rumus jadi bait-bait syair

Bila rumus-rumus dan operasi aritmetika
disamarkan sebagai adegan-adegan tentang
pangeran, putri, kurcaci dan naga
untuk anu, begitu, begini dan 1

di mana menari pelambang bagi PLUS
dan duduk jadi pelambang bagi MINUS
maka rumus bagi silogisme Barbara
bisa diuntai sebagai bait-bait syair

{ini bait pelambang premis minor}

Seorang kurcaci dan seekor naga
di atas panggung keduanya menari
ditonton oleh seorang pangeran
duduk sendiri di luar gelanggang

{dan bait pelambang penggabung DAN}

Kemudian datanglah seekor naga
segera duduk ikut menonton,
dan menunggu tamu berikutnya yang 
akan datang masuk ke gelanggang

{serta bait pelambang premis major}

Lalu datang putri dan seekor naga
keduanya ke panggung ikut menari
lalu datang lagi seorang kurcaci
yang ikut duduk bersama pangeran,

{inilah bait pelambang deduksi}

Tiba-tiba naga yang duduk menonton
bangkit menyerang naga penari
keduanya pun segera berkelahi
menghilang setelah keduanya mati

Namun kemudian kurcaci yang duduk 
bangkit mengajak kurcaci penari
untuk keluar dari dalam gelanggang
keduanya menghilang ke dalam hutan

{dan ini bait pelambang konklusi}

Tinggal pangeran duduk sendiri
menonton sang puteri dan naga
yang sedang menari bersama-sama
bergembira sambil beryanyi-nyanyi

{akhirul kata}

Itulah kisah yang diceritakan
oleh Ni Suiti pada Si Ome cucunya
untuk mengajarkan silogisme Barbara.
begitulah alur ceritanya.

Dialog tentang Silogisme Boole

DIALOG TENTANG SILOGISME BOOLE

Armahedi Mahzar (c) 2016 

George Boole

Ki Algo baru saja menemukan sebuah metoda untuk menentukan keabsahan sebuah silogisme dengan menggunakan notasi asli George Boole untuk operasi-operasi logika. Metoda itu sangat mudah: cukup menghitung nilai rumus silogisme dengan notasi Boole tersebut. Jika hasilnya sama dengan 1, maka silogisme itu absah atau benar. Jika tidak berari tidak absah.

Ki Algo sangatlah gembira, karena George Boole sendiri tidak mengetahui metoda yang ditemukannya tersebut. Lalu dia pun menemui Ni Suiti, istrinya, untuk memamerkan penemuan yang menurutnya luar biasa itu. Berikut adalah dialog antara kedua suami istri kakek nenek itu. Kalau anda sudah lulus SMP, pastilah bisa memahaminya :)

Ki Algo: Mau belajar logika cara mudah?
 

Ni Suiti: Wah, memangnya logika mudah? Saya sudah baca risalahnya Aristoteles, pusingnya setengah mati.

Ki Algo: Mudah kalau kamu belajar aljabar Boole.

NOTASI ASLI ALJABAR BOOLE

Ni Suiti: Ya, aljabar boole memang mudah karena hanya ada dua bilangan yaitu 1 dan 0. Tapi saya bingung baca keterangan Boole di bukunya Laws of Thought tentang silogisme. Rumusnya tentang kesimpulan sebuah silogisme umum sangatlah panjang dan kompleks. Saya gagal paham.

Ki Algo: Ya, jangan baca itu. Boole memang mau pecahkan silogisme Aristoteles dengan cara aljabar. Makanya jadi susah. Saya punya cara yang mudah.

Ni Suiti:  Bagaimana tuh?

Ki Algo: Saya akan pakai notasi asli Boole untuk logika. TIDAK x ditulis sebagai 1-x. Sedangkan x ATAU y ditulis sebagai x + y. Jadi TIDAK bisa diganti dengan '1-' dan ATAU bisa diganti dengan '+'.

Ni Suiti: Ya, itu sih saya tahu. Pernyataan logis x DAN y ditulis sebagai xy (x KALI y).

Ki Algo: Memang begitu cara berpikir Boole. Tapi kalau dia tidak menganggap perkalian sebagai operasi fundamental, maka aritmetika logika menjadi lebih sederhana.

Ni Suiti:  Oh, ya. Mana bisa?

Ki Algo: Pakai saja hukum de Morgan TIDAK (x DAN y) = TIDAK x ATAU TIDAK y

1-(xy)= 1-x+1-y. Kalau ini diselesaikan, kita dapat xy=x-1+y.

Jadi DAN bisa diganti dengan '-1+'.

Ni Suiti:  Hahaha, bagus juga tuh. Bagaimana dengan JIKA p MAKA q?

Ki Algo: Ganti saja JIKA dengan '1-' dan ganti MAKA dengan '+'. Jadi rumus Boole untuk JIKA p MAKA q adalah 1-p+q.

Ni Suiti:  Wah, saya gak pernah lihat itu di bukunya Boole.

Ki Algo: Itulah dia, Boole terobsesi dengan aljabar. Jadi dia tak memerlukan penulisan aritmetika untuk operasi JIKA dan MAKA. Padahal, kalau dia membebaskan dirinya dari obsesi itu, dia akan lebih mudah menganalisis silogisme Aristoteles.

RUMUS UMUM SILOGISME

Ni Suiti: Ya. Silogisme Aristoteles JIKA alasan1 DAN alasan2 MAKA kesimpulan. Dengan rumus kamu silogisme itu jadi 1-(alasan1-1+alasan2)+kesimpulan = 1-alasan1+1-alasan2+kesimpulan.

Ki Algo: Dengan rumus ini, kita hanya memeriksa apakah ini menghasilkan 1 yang menurut Boole adalah lambang untuk BENAR. Jika hasilnya sama dengan satu silogisme itu ABSAH atau BENAR.

RUMUS PERNYATAAN ARISTOTELES

 

Ni Suiti:  Tapi, bagaimana kita menyatakan pernyataan kategoris Aristoteles secara matematis?

Ki Algo:Maccoll menyatakan bahwa pernyataan SEMUA a ITU b itu sama dengan pernyataan JIKA a MAKA b jadi rumusnya adalah 1-a+b. Mudah bukan?

Ni Suiti: Kalau SEMUA a TIDAK b?

Ki Algo: Tentu saja 1-a+1-b.

Ni Suiti:  Kalau SEBAGIAN a ITU b?

Ki Algo: SEBAGIAN a TIDAK b itu sama dengan TIDAK SEMUA a TIDAK b. Jadi rumusnya adalah 1-(1-a+1-b) atau a-1+b.

Ni Suiti:  kalau SEBAGIAN A TIDAK b?

Ki Algo: Tentu saja a-1+1-b atau a-b.

PEMBUKTIAN SILOGISME

 

Ni Suiti:  OK, coba lihat saya punya silogisme JIKA SEBAGIAN a ITU b DAN SEBAGIAN c TIDAK b MAKA SEBAGIAN a ITU c.

Ki Algo: Seperti dikatakan terdahulu rumus umum silogisme adalah

1-alasan1+1-alasan2+kesimpulan.

Untuk silogismemu rumusnya

1-(a-1+b)+1-(c-b)+(a-1+c) yang kalau dievaluasi

1- a+1-b +1- c+b + a-1+c hasilnya sama dengan 2.

Jadi silogisme itu nilainya tidak sama dengan 1. Dengan demikian dia tidak benar.

Ni Suiti:  Coba sekarang dengan silogisme Barbara ini JIKA SEMUA b ITU c DAN SEMUA a ITU b, MAKA SEMUA a ITU c!

Ki Algo:Rumus silogisme ini adalah

1-(1-b+c)+1-(1-a+b)+1-a+c. Dievaluasi jadi

1- 1+b-c +1- 1-a-b +1-a+c

dan hasilnya adalah 1. Jadi silogisme Barbara itu BENAR atau ABSAH.

Ni Suiti:  Wah, terima kasih. Saya akan coba untuk semua silogisme absah yang ada dalam tabel silogisme Leibniz ini.

Tabel Silogisme Leibniz

Ki Algo: Wow, jumlah silogisme dalam tabel itu ada 24. Untuk mempermudah pembuktianmu, evaluasi saja rumus bagi alasan1 DAN alasan2 jika hasilnya adalah rumus dari kesimpulan, maka silogisme itu absah

Ni Suiti: OK  '

DIALOG AKHIR 

Setelah mencoba keampuhan metoda Ki Algo itu, besoknya Ni Suiti menemui Ki Algo dan mengatakan begini

Ni Suiti: Wow, metodamu benar-benar ampuh dan mudah karena bisa dipelajari oleh anak SMP. Tapi, alhamdulillah, diilhami dari dari metodamu itu aku bisa mentransformasi metodamu menjadi berbagai permainan barang yang bisa dimainkan anak TK dengan mudah.

Ki Algo: Huh, bagaimana bisa?

Ni Suiti:  Lain kali saja yah penjelasannya?

Ki Algo: Baiklah. Aku sabar menanti.

Sejarah Masuknya Islam di Australia

Sejarah Masuknya Islam di Australia

Bilal Cleland

CANBERRA--Ternyata Islam telah tiba di Australia sejak abad ke-16 dan 17 M, sebelum permukiman Eropa hadir. Pengunjung pertama yang singgah di benua itu adalah Muslim yang berasal dari Indonesia timur.

Bilal Cleland dalam bukunya berjudul The Muslim in Australia A Brief History mengungkapkan, nelayan dan pedagang Muslim asal Makassar sudah melego jangkar di pesisir utara Australia Barat dan Australia Utara sekitar 1650 M. Ketika itu, orang Makassar telah menjalin hubungan dagang dengan penduduk asli. Adanya kesamaan beberapa kata dalam bahasa Makassar dengan bahasa penduduk asli di pesisir Australia merupakan bukti hubungan kedua budaya. Pemerintah Australia pun telah mengakui dan mencatat kehadiran Muslim asal Indonesia Timur sebagai pengunjung awal negeri itu dalam sejarah mereka.

Migran Muslim dari pesisir Afrika dan wilayah pulau di bawah Kerajaan Inggris, juga mulai berdatangan ke Australia sebagai pelaut dan narapidana. Mereka datang ke negeri itu pada akhir dasawarsa 1700-an. Berdasarkan catatan sejarah resmi Australia, populasi Muslim semipermanen pertama datang ke Australia dalam jumlah yang signifikan pada dasawarsa 1800-an.

Mereka adalah penunggang unta yang datang dari anak benua India. Kehadiran Muslim penunggang unta asal Afghanistan itu dinilai telah memberi kontribusi yang sangat besar bagi penjelajahan awal pedalaman Australia dan pembentukan jaringan perhubungan. Jumlah umat Islam di Australia modern terus bertambah pesat setelah meletusnya Perang Dunia II.

Berdasarkan catatan resmi Pemerintah Australia, pada 1947-1971, populasi Muslim melonjak dari 2.704 jiwa menjadi 22.331. Akibat ledakan ekonomi pascaperang, banyak umat Muslim Eropa, terutama dari Turki, mencari kehidupan dan rumah baru di Australia.

Menurut Chamandeep Chehl, direktur National Action Plan (NAP) Multicultural Affairs Branch pada Departemen Imigrasi dan Kewarganegaraan Australia, jumlah umat Muslim di negara itu berdasarkan sensus 2006 mencapai 340 ribu jiwa dari sekitar 21 juta total jumlah penduduk negeri itu.

Muslim di Australia terbilang unik. Umat Muslim di negeri itu terbilang sangat majemuk karena berasal dari 120 negara. ''Alhamdulillah, jumlah umat Islam di Australia terus bertambang dari tahun ke tahun,'' ujar Ahmed Youssef, tokoh Muslim di Canberra Islamic Centre, saat bertemu dengan tiga tokoh Muslim muda asal Indonesia, yakni; Cucu Surahman, dosen UIN Syarif Hidayatullah Jakarta; Muhammad Subhan Setowara, dosen Universitas Muhammadiyah Kupang, NTT; dan Mohammad Hasan Basri, peneliti pada Centre for Religious and Cross Culture Studies (CRCS) Yogyakarta.

Menurut Youssef, yang telah menetap di Australia selama 40 tahun, umat Muslim sangat menikmati kebebasan beragama di Australia. ''Dibanding di negara kelahiran saya, Australia sangat menghormati kebebasan beragama. Di sini, Anda dapat menulis dan berpikir dengan bebas,'' tutur imigran asal Mesir itu menuturkan.

Kini, tak kurang dari 140 masjid dan mushala bertebaran di kota-kota Australia. ''Warga Australia yang tertarik untuk masuk Islam pun terus meningkat,'' papar Imam Besar Masjid Emir Sultan di Dandenong, Victoria, Mehmed Salih Dogan. Ia pun mengakui betapa Australia menghormati kebebasan beragama.

''Kita bisa shalat di mana saja. Orang Australia menghormatinya,'' tutur Faqihuddin Abdul Kodir, seorang dosen asal Indonesia yang tengah menimba ilmu di Australian National University (ANU) Canberra. Kini, sekolah-sekolah Islam sudah mulai tersebar di seantero Australia. Rumah makan halal pun menjamur dan begitu diminati setiap orang di negeri itu.

Bahkan, bank syariah pun sudah mulai diperkenalkan di negeri itu. Muslim Australia diakui telah memberi sumbangsih penting dalam bidang usaha sosial, ekonomi, kebudayaan, keagamaan, dan pendidikan.

Begitu majemuknya umat Muslim di Australia, ternyata masih menyisakan masalah. ''Sebagian umat Islam terpecah berdasarkan etnis. Padahal, yang harus mereka utamakan adalah keislamannya, baru setelah itu dari mana mereka berasal. Inilah tantangan kita,'' tutur Youssef. heri/RioL

- http://en.wikipedia.org/wiki/Islam_in_Australia

Sejarah Masuknya Islam/Muslim ke Australia

Sejarah masuknya Islam ke Australia dimulai dari interaksi pertama kali nelayan yang berasal dari Sulawesi Selatan (Indonesia) dengan penduduk asli di bagian Utara Australia (Aborigin) pada sekitar tahun 1750. Tidak banyak jumlah Muslim yang tinggal di Australia saat itu, sampai pada sekitar tahun 1860 serombongan penggembala onta berasal dari Afganisthan datang ke Australia menambah jumlah Muslim yang tinggal di Australia.

Pada abad ke 19 Australia mempunyai banyak daerah/tanah yang kaya akan sumber daya alam yang belum tereksploitasi.Sebagian besar dari tanah tersebut berupa padang pasir dengan temperatur yang sangat tinggi dengan sedikit sumber mata air. Onta merupakan binatang ideal untuk kondisi tersebut, maka pada tahun 1840 seorang bernama Horrick memasukkan (import) pertama kali onta ke Australia, dia ingin membandingkan antara onta dan kuda sebagai hewan pengangkut barang di padang pasir, tetapi missi ini gagal. Kelompok onta selanjutnya datang pada tahun 1860 sebanyak 24 onta. Dengan mencoba mempergunakan onta sebagai hewan pengangkut, Australia membutuhkan orang-orang yang ahli dalam mengendarai dan mengoperasikan onta, maka didatangkanlah untuk pertama kali orang-orang Afghanistan untuk mengoperasikan 24 onta tersebut, dan tidak lama setelah itu berdatangan lebih banyak Muslim Afghanisthan ke Australia. Sekitar 10.000 sampai 12.000 onta didatangkan ke Australia dalam kurun waktu antara tahun 1860 sampai 1907.

Sekitar 3000 orang Muslim berasal dari Afghanistan bekerja sebagai pengangkut barang-barang, air, serta makanan dengan mempergunakan onta di daerah-daerah yang sulit. (A. Saeed, Islam in Australia, Allen & Unwin, 2003). Para penggembala onta dari Afghanistan ini menemukan tempat yang hampir sama kondisinya seperti di daerah asal mereka di Australia tengah, mereka mengendarai ontanya dan berjalan melintasi padang pasir sekitar 600 km untuk mengangkut barang-barang kebutuhan utama dan penting dari Oodnadatta menuju Alice Springs (Australia Tengah). “Kontribusi mereka dalam membuka areal serta jalur umum untuk masyarakat luas di daerah-daerah Australia sangat besar dan penting. Tulang punggung perekonomian tradisional Australia saat itu yaitu agriculture dan pertambangan sangat membutuhkan onta sebagai alat transportasi beserta penggembalanya” (Tin Mosques and Ghantowns – Christine Stevens 1989).

Dengan berakhirnya era transportasi industri mempergunakan onta pada sekitar tahun 1920, serta peraturan yang lebih ketat dari badan Imigrasi Australia berkenaan dengan sedikitnya populasi warga kulit putih Australia, maka jumlah Muslim Afghanistan yang dating ke Australia menjadi berkurang. (B. Cleland, The Muslims in Australia: A Brief History, Islamic Council of Victoria, 2002).

Pada sekitar tahun 1960, disebabkan peraturan yang lebih longgar dari badan Imigrasi Australia berkenaan dengan migrasi bangsa non-Eropa ke Australia, jumlah Muslim yang datang ke Australia menjadi bertambah. Pada sekitar tahun 1960 dan sekitar tahun 1970 dalam jumlah yang cukup besar terjadi migrasi Muslim dari Lebanon dan Turki ke Australia, dimana jumlah Muslim terbesar di Australia saat ini berasal dari ke dua Negara tersebut.

Jumlah Muslim terbesar yang tinggal di Australia saat ini berasal dari bangsa Arab, dibandingkan dengan bangsa Arab lainnya Muslim yang berasal dari Lebanon mempunyai jumlah terbesar dan sejarah migrasi yang lebih panjang/lama. Migrasi pertama bangsa Libanon ke Australia terjadi pada sekitar akhir tahun 1880-an.

Gelombang kedua migrasi terjadi antara tahun 1947 sampai dengan 1975, terutama setelah terjadi perang antara bangsa Arab dan Israel pada tahun 1967. Gelombang ke tiga terjadi pada tahun 1976 setelah terjadi perang sipil di Lebanon. Bangsa Arab lain yang mempunyai populasi terbanyak di Australia adalah dari Mesir. Seperti halnya bangsa Lebanon, migrasi bangsa Mesir ke Australia terbesar terjadi setelah perang dunia II, migrasi ini terjadi dalam dua gelombang yaitu antara tahun 1947 sampai dengan 1971, dan gelombang ke dua terjadi pada sekitar akhir 1980-an. (A. Saeed, Islam in Australia, Allen & Unwin, 2003).

Muslim di Australia saat ini

Berdasarkan sensus dari Australian Bureau of Statistics (ABS) pada tahun 2001, jumlah Muslim di Australia sebesar 281.578 orang, atau 1,5 % dari populasi jumlah penduduk Australia. Sedangkan menurut estimasi dari salah satu lembaga Islam di New South Wales (NSW) mencapai 300.000 orang. Sensus juga menunjukkan bahwa Muslim di Australia berasal dari berbagai Negara, dengan hanya 20,8 % berasal dari Lebanon dan 14.5 % berasal dari Turki, sedangkan 64.7 % berasal dari sekitar 9 negara (Indonesia, Afghanistan, Bosnia, dsb). Sensus tersebut juga menunjukkan bahwa Muslim Australia mempunyai pendidikan yang cukup baik dibandingkan dengan penduduk Australia secara keseluruhan, 21,7 % dari Muslim Australia yang berusia di atas 15 tahun mempunyai gelar sarjana (bachelor degree) atau lebih tinggi, prosentase ini lebih tinggi dibandingkan dengan 12,4 % dari penduduk Australia secara keseluruhan. Kesimpulan penting dari hasil statistik ini adalah bahwa anggapan negatif tentang mayoritas Muslim Australia tidak berpendidikan terutama yang berasal dari bangsa Arab adalah tidak berdasar.

Aktifitas Ibadah

Dalam melakukan aktifitas ibadah Muslim di Australia mempunyai lebih dari 85 Masjid dan sekitar 50 musolah (tempat sholat), disamping itu di beberapa daerah yang jauh dari Masjid beberapa Muslim berinisiatif untuk menyewa gedung (misalnya gedung pusat kegiatan komunitas) untuk dijadikan tempat sholat jum’at. Untuk membangun sebuah Mesjid memerlukan prosedur tertentu yang telah ditetapkan oleh pemerintah yang harus dipenuhi syarat-syaratnya sebagaimana membangun gedung-gedung untuk kepentingan umum lainnya.

Secara individual biasanya Muslim mempunyai masalah dalam melakukan aktifitas ibadah sholat pada saat hari kerja, yang paling banyak mengalami masalah adalah pada saat pelaksanaan shalat Jum’at. Apabila menghadapi masalah sulitnya melaksanakan sholat Jum’at, muslim yang taat memilih keluar dari tempat kerja atau mengorganisasi beberapa muslim yang berdekatan tempat kerjanya untuk melaksanakan sholat Jum’at, sedangkan muslim yang kurang taat melaksanakan ibadahnya memilih meninggalkan sholat Jum’at. Kegiatan keagamaan di Australia cukup semarak, hal ini bias dilihat dari banyaknya majelis taklim atau kelompok-kelompok pengajian yang ada, bahkan beberapa gerakan Islam cukup aktif terlihat melakukan berbagai aktifitas.

Kondisi Muslim Australia Pasca Bom London 7 Juli 2005

Tidak lama setelah terjadi peristiwa meledaknya bom di London 7 Juli 2005, pemerintahan Negara Barat segera melakukan kampanye terus menerus untuk memberlakukan undang-undang khusus bagi umat Islam yang tinggal di Negara Barat. Mereka mencoba membentuk opini menyesatkan kepada masyarakat bahwa undang-undang baru tersebut dimaksudkan untuk melindungi dan memerangi bahaya serangan terorisme di Negara mereka. Tetapi tidak bisa dielakkan, agenda tersembunyi dari kampanye tersebut yaitu membidik serta melemahkan Islam dan Muslim di Negara Barat segera terlihat nyata.

Strategi dan agenda tersembunyi yang ditunjukkan oleh Pemerintahan Negara Barat mempunyai banyak kesamaan. Propaganda yang dimulai dengan alasan yang dicari-cari untuk memerangi terorisme, segera diperluas untuk memerangi apa yang mereka sebut dengan pendapat/ide radikal dan ekstrim, strategi ini ditargetkan untuk memecah belah Muslim dengan memberi predikat muslim moderat dan muslim radikal/ekstrim.

Di Australia target juga diarahkan ke sekolah-sekolah muslim, dimana pemerintah akan meninjau kembali kurikulum yang diajarkan di sekolah-sekolah tersebut. Rencana ini segera mendapat reaksi keras dari sekolah-sekolah muslim, karena kurikulum yang diajarkan saat ini tidak beda jauh dengan apa yang diajarkan di sekolah-sekolah lainnya, bahkan banyak murid dari sekolah-sekolah muslim tersebut yang mempunyai prestasi lebih tinggi dibandingkan dengan sekolah lainnya. Pemerintah juga mengusulkan agar di sekolah-sekolah muslim lebih banyak diajarkan nilai-nilai kemasyarakatan Australia, seperti toleransi, tanggung jawab dan sebagainya, dimana nilai-nilai tersebut juga ada dalam Islam dan sudah diajarkan di sekolah-sekolah muslim tersebut, lebih dari itu sekolah-sekolah muslim dalam kurikulum belajar tidak pernah mengajarkan tindakan terorisme. Sedangkan di masjid-masjid, pemerintah mengusulkan agar para Imam masjid diberi pengarahan apa yang seharusnya boleh mereka ceramahkan.

Tidak hanya sampai disitu, anggota parlemen dari partai Liberal Bronwyn Bishop mengusulkan agar melarang pemakaian jilbab di sekolah-sekolah umum, karena jilbab dianggap bertentangan dengan nilai-nilai kemasyarakatan Australia tentang persamaan dan menyebabkan perpecahan di sekolah-sekolah. Usulan ini juga mendapat tantangan keras baik dari muslim maupun non muslim, sebagian besar yang menentang usulan itu mengatakan bahwa tidak ada bukti pemakaian jilbab di sekolah-sekolah menyebabkan perpecahan dan persamaan hak. Kerry Cullen salah satu kepala sekolah menengah umum tingkat atas (SMTA) di Sydney mengatakan bahwa di sekolahnya hanya ada satu orang yang menggunakan jilbab merah kecoklatan dimana warna tersebut sesuai dengan seragam sekolahnya, dan itu bukan suatu masalah di lingkungan sekolahnya. Tidak pernah ada laporan negatif dari guru-guru atau murid-murid yang disebabkan oleh pemakaian jilbab. Kepala sekolah lainnya mengatakan bahwa kita tidak pernah melihat adanya perpecahan yang disebabkan oleh pemakaian jilbab, kami melihatnya sebagai sebuah keragaman budaya.

Hubungan Muslim dan Non Muslim serta harapan Muslim di Australia

Secara umum hubungan Muslim dan Non Muslim di Australia cukup baik, terutama sebelum terjadi peristiwa 11 September. Tetapi setelah peristiwa 11 September, bom bali, kemudian disusul bom London banyak Muslim yang mendapat perlakuan kurang menyenangkan baik oleh masyarakat umum maupun oleh pemerintah dan media massa. Namun demikian hubungan personal antara Muslim dan Non Muslim masih cukup baik, meskipun terkadang sebutan teroris baik dalam nada bercanda maupun serius sering dilontarkan Non Muslim kepada Muslim, sebutan atau label teroris ini terkadang kurang menyenangkan bagi Muslim.

Secara umum harapan Muslim yang tinggal di Australia adalah bisa lebih mudah menjalankan aktifitas ibadahnya terutama ibadah sholat Jum’at, sedangkan harapan yang ditujukan kepada pemerintah Australia dan media massa adalah tidak terus menerus menyudutkan Muslim dengan memberi label-label yang tidak menyenangkan seperti ekstrimis, radikal, teroris dan sebagainya. (Bambang Purba Kencana)

sumber :swaramuslim.net

Bermain Kartu Silogisme Boole

Bermain Kartu Silogisme Boole

Armahedi Mahzar © 2016

Logika adalah ilmu tentang penalaran yang dirumuskan dalam untaian kata-kata oleh Aristoteles yang membungkus huruf-furuf yang melambangkan pengertian. George Boole mengganti bungkus kata-kata itu dengan bungkus tanda-tanda ilmu hitung dalam bentuk persamaan aljabar yang mungkin bisa dipelajari oleh siswa SMP.

Untuk menyederhanakannya, pada artikel yang lalu, saya mengajukan sebuah sistem aritmetika logika Boole sebagai aritmetika alias ilmu hitung. Sistem itu mungkin bisa diajarkan pada seorang murid SD.

Akan tetapi, sistem itu pasti tidak bisa diajarkan pada anak TK yang belum bisa membaca atau menghitung. Berikut ini adalah sebuah permainan menggunakan kartu berwarna dan kartu-kartu hitam dengan ilmu kombinatorik alias ilmu gabung-menggabung. Saya kira permainan ini bisa diajarkan di TK.

Susun-susun Kartu Berwarna

Untuk itu kita memerlukan tiga macam kartu berwarna berbeda dan beberapa buah kartu berwarna hitam. Beberapa dari kartu-kartu tersebut bisa saya susun menjadi empat kumpulan kartu yang sah yang kemudian akan bisa digunakan dalam permainan silogisme. Keempat macam susunan kartu yang sah itu mempunyai nama keempat guruf hidup pertama dalam alfabet: A, E, I dan O. Kita sebut saja kumpulan kartu sebagai kumpulan Aristo-Boole.

Kumpulan kartu A terdiri dari 1 kartu hitam tegak, 1 kartu berwarna tidur dan 1 kartu berwarna lain tegak. Sedangkan kumpulan kartu E terdiri dari 2 kartu hitam tegak, 1 kartu berwarna tidur dan 1 kartu berwarna lain tegak. Selanjutnya kumpulan kartu I terdiri dari 1 kartu hitam tidur, 1 kartu berwarna tegak dan 1 kartu berwarna lain tegak. Akhirnya kumpulan kartu O terdiri dari 1 kartu berwarna tegak dan 1 kartu berwarna lain tidur.

Ringkasnya ada pada tabel kumpulan Aristo-Boole berikut ini

Tabel Aristo-Boole

Susunan kartu di atas adalah disebut sah karena melambangkan semua pernyataan kategoris Aristoteles. Susunan kartu ini akan digunakan dalam permainan silogisme berikut ini.

Permainan Kartu Silogisme

Aristoteles menggabung dua pernyataan kategoris yang menghubungkan tiga pengertian, jika keduanya menyimpulkan satu hubungan kategoris antara dua pengertian yang tidak dimiliki bersama oleh kedua alasan tersebut, maka ketiga pernyataan itu disebutnya sebagai sebuah silogisme.

Permainan silogisme adalah menggabungkan dua buah susunan sah kartu yang mmengandung kartu-kartu dengan tiga warna berbeda, sebagai pelambang dari dua buah alasan, dan mencari kesimpulan dengan cara membuang pasangan kartu tegak/tidur. Permainan silogisme ini terdiri dari dua tahap:

Tahap pertama adalah penggabungan alasan terdiri dari 3 langkah

1. Buatlah susunan kartu yang sah dengan memakai dua kartu berwarna\
2. Tambahkanlah sebuah kartu hitam tidur sebagai penggabung
3. Tambahkanlah susunan sah yang lain menggunakan kartu yang warnanya sama dengan salah satu warna kartu yang ada pada susunan pertama dan kartu yang warnanya berbeda dari kedua warna kartu yang ada pada susuna pertama.

Tahap kedua adalah pengambilan kesimpulan dengan cara 

• Membuang semua pasangan kartu yang berwarna sama tapi beda posisi 

 Jika hasilnya menyisakan sebuah gabungan kartu yang sah, maka nergembiralah anda, karena anda susunan kartu awal anda adalah pelambang bagi gabungan dua alasan sebuah silogisme yang absah. Jika tidak, maka silogismme yang dilambangkan oleh kartu-kartu itu dianggap tidak absah.

Contoh permainan Yang Gagal

Kumpulan AO yaitu Agb DAN Org Kesimpulannya ternyata tidak sah, jadi silogismenya tidak absah alias tidak benar.

Silogisme tak absah                                        kesimpulan tak sah

Pada umumnya, permainan silogisme akan berhasil jika silogismenya benar yang diperoleh dengan mengikuti dua larangan (1) kartu berwarna sama pada kedua alasan tidak boleh sama posisinya. (2) susunan kartu bagi kedua alasan tidak boleh sama-sama berada pada kolom atau baris kedua pada tabel susunan sah Aristo-Boole. Anda bisa mencoba dan melihat bahwa jika kita mengikuti kedua larangan tersebut maka kita akan memperoleh kesimpulan yang sah.

Contoh Permainan Yang Berhasil

Kumpulan kartu AA melambangkan Agb DAN Arg di mana pengertian r, g dan b dilambangkan oleh kartu merah, hijau dan biru. Ruas paling kiri dari persamaan berikut ini adalah susunan kartu tersebut.

Silogisme Barbara

Ruas kedua diperoleh setelah membuang pasangan kartu tegak/tidur hasilnya adalah susunan sah lambang Arb yang mengkodekan pernyataan SEMUA r ITU b. Untuk bisa melihatnya kita dekatkan kartu-kartu satu sama lainnya, sehingga tampak bahwa susunan itu benar-benar sah. Inilah silogisme Barbara. Pelambang gabungan alasan pada silogisme absah lainnya ada pada tabel berikut ini

Tambel Silogisme Universal

Dalam tabel berikut ini terdapat lambang bagi silogisme dengan dua alasan universal yang memerlukan eksistensi pengertian x yang dilambangkan oleh SEBAGIAN x ITU x sehingga menghasilkan kesimpulan partikular.

Tabel Silogisme Eksistensial

Catatan Akhir

1. Tentu saja, permainan ini bisa dijadikan permainan dengan balok-balok berdimensi tiga yang juga berwarna-warni sehingga lebih asyik untuk dimainkan oleh anak-anak pra TK.
2. Untuk anak-anak SD, kartu-kartu warna-warni ini bisa diganti dengan kartu-kartu bridge dan kartu warna hitam diganti dengan kartu tertutup dan kartu berwarna diganti dengan kartu terbuka dengan tanda gambar yang berbeda.
3. Untuk anak-anak SMP, permainan kombinatorik kartu-kartu ini bisa diubah menjadi permainan kombinatorik tanda dan huruf-huruf yang dituliskan. Kartu hitam tegak diganti dengan tanda “|” sedangkan kartu hitam tidur diganti dengan tanda titik “.” . Kartu berwarna tegak diganti dengan huruf kecil x sedangakan yang tidurSilogisme diganti dengan huruf besar X. Pembuangan kartu diganti dengan pencoretan tanda huruf. Kesimpulan adalah kumpulan tanda yang tak tercoret.
4. Permainan kartu berwarna dan berbagai modifikasi yang disebut di atas bersifat soliter yang hanya dimainkan oleh satu orang. Saya minta tolong pada para pembaca untuk menyusun permainan kompetitif lebih dari dari satu orang berdasarkan permainan soliter di atas sehingga bisa dikompetisikan. Kompetisi itu diharapkan bisa meningkatkan IQ para pemain beberapa point seperti permainan WFF ‘N PROOF ciptaan professor Layman E. Allen dari fakultas hukum Yale University di Amerika Serikat.

Mengenang Soempah Pemoeda

PARA pemuda dari hampir semua suku bangsa di wilayah India-Belanda mendirikan berbagai organisasi yang masih berlatar belakang wilayah atau etnis, seperti Jong Sumateranen Bond, Jong Java, Jong Batak, Jong Minahasa, Jong Ambon, Jong Islamieten Bond, Pemoeda Kaoem Betawi, Jong Celebes, Jong Indonesia (Pemuda Indonesia) dan Sekar Rukun. 

 

Dari tanggal 30 April – 2 Mei 1926 di Jakarta diselenggarakan Kongres Pemuda I, namun pada Kongres tersebut, belum berhasil mempersatukan seluruh organisasi pemuda Indonesia. Setelah Kongres Pemuda I, pada bulan September 1926, beberapa mahasiswa jurusan hukum dan kedokteran mendirikan Perhimpunan Pelajar-Pelajar Indonesia (PPPI). PPPI kemudian mengadakan pendekatan ke sejumlah organisasi pemuda dan mengusulkan diselenggarakannya Kongres Pemuda II.

Pada bulan Juli 1928, disetujui pembentukan Panitia Kongres Pemuda II dengan susunan sebagai berikut: Ketua : Sugondo Joyopuspito (PPPI) Wakil Ketua : Joko Marsaid (Jong Java) Sekretaris : Muhammad Yamin (Jong Sumateranen Bond) Bendahara : Amir Syarifuddin Harahap (Jong Batak) Pembantu I : Johan M. Cai (Jong Islamieten Bond) Pembantu II : Katjasungkana (Pemuda Indonesia) Pembantu III : Senduk (Jong Celebes) Pembantu IV : Josef Leimena (Jong Ambon) Pembantu V : Rohyani (Pemoeda Kaoem Betawi) Mereka memperoleh dukungan dan nasihat dari sejumlah tokoh yang lebih tua antara lain Mr. Sartono, Mr. Muhammad Nazief, Mr. Arnold I.Z. Mononutu dan Mr. Sunario.

Pada 27 dan 28 Oktober 1928 -juga di Jakarta- diselenggarakan Kongres Pemuda II, dihadiri sekitar 750 pemuda dari berbagai organisasi. Jong Java dipimpin oleh Joko Marsaid, Jong Islamieten Bond dipimpin oleh Johan M. Cai, Jong Sumateranen Bond dipimpin oleh Muhammad Yamin, Jong Batak dipimpin oleh Amir Syarifuddin Harahap, Pemuda Indonesia dipimpin oleh Katjasungkana (ayahanda dari Nursyahbani Katjasungkana, anggota DPR RI 2004-2009 dari Fraksi PKB), Jong Celebes dipimpin oleh Senduk, Jong Ambon dipimpin oleh Josef Leimena, dan Pemoeda Kaoem Betawi dipimpin oleh Rohyani.

Sejumlah tokoh yang lebih tua yang ikut hadir antara lain Mr. Sartono, mewakili PNI Cabang Jakarta, Kartakusuma mewakili PNI Cabang Bandung, Abdulrachman mewakili Budi Utomo Cabang Jakarta, Mr. Sunario mewakili PAPI (Persaudaraan Antara Pandu Indonesia) dan INPO, Arnold Mononutu mewakili Persatuan Minahasa, Sigit mewakili Indonesische Club, Muhidin mewakili Pasundan dan Sekarmaji Marijan Kartosuwiryo mewakili Pengurus Besar PSI (Partai Sarikat Islam).

(Catatan:
1. Amir Syarifuddin Harahap kemudian menjadi Perdana Menteri RI kedua. Bulan September 1948 Amir terlibat dalam peristiwa Madiun, yang oleh Jenderal T.B. Simatupang disebut sebagai tragedi nasional. Amir Syarifuddin ditangkap dan dieksekusi pada 20 Desember 1948, sehari setelah Belanda melancarkan agresi militer ke dua.
2. Sekarmaji Marijan Kartosuwiryo pada bulan Agustus 1949 memproklamasikan berdirinya Negara Islam Indonesia. Kartosuwiryo ditangkap dieksekusi tahun 1962)

Selain itu hadir juga kaum nasionalis Indonesia seperti S. Mangunsarkoro, Nona Purnomowulan, Mr. Mohammad Nazief, Siti Sundari, E. Puradireja, Kuncoro Purbopranoto, Sukmono, Suryadi, Jaksodipuro (Wongsonegoro), Muhammad Rum, Dien Pantouw, Suwiryo, Sumanang, Dali, Syahbudin Latif, Sulaiman Kartomenggolo, Sumarto, Masdani, Anwari, Nona Tumbel, Tamzil, A.K. Gani, Jo Tumbuan, Pangemanan, Halim, Antapermana, Suwarni dan Kasman Singodimejo. 

Anggota Volksraad yang hadir adalah Suryono dan Sukowati. Selain Polisi-polisi Belanda juga selalu dalam setiap sidang dengan senjata lengkap, Pemerintah Belanda mengutus Dr. Pyper dan Dr. Charles Olke van der Plas untuk hadir dalam Kongres tersebut.

Rapat pertama diselenggarakan di gedung Katholieke Jongelingen Bond, Waterlooplein . Sebelum dibuka, dibacakan amanat tertulis Ir. Soekarno , Ketua PNI, amanat Perhimpunan Indonesia di negeri Belanda, dan juga amanat Tan Malaka . Dalam sambutannya, ketua PPPI Sugondo Djojopuspito berharap kongres ini dapat memperkuat semangat persatuan dalam sanubari para pemuda. 

Dalam acara sambutan, terjadi dua kali insiden.

Yang pertama terjadi ketika seorang pembicara mempergunakan kata “kemerdekaan” yang mengakibatkan polisi Belanda menegur ketua sidang dan mengancam akan mengeluarkan semua pemuda di bawah usia 18 tahun, karena menganggap pertemuan ini adalah rapat politik.

Insiden kedua timbul, karena seorang pembicara menganjurkan agar Indonesia menjadi suatu negeri seperti Inggris, Jepang dll. Perbandingan ini juga membuat polisi Belanda melakukan peneguran kepada ketua sidang dan meminta agar semua pemuda di bawah 18 tahun dikeluarkan dari ruang sidang. Namun permintaan tersebut ditolak oleh ketua sidang.

Acara dilanjutkan dengan uraian Moehammad Yamin tentang arti dan hubungan persatuan dengan pemuda. Menurutnya, ada lima faktor yang bisa memperkuat persatuan Indonesia yaitu sejarah, bahasa, hukum adat, pendidikan, dan kemauan.

Rapat kedua tanggal 28 Oktober, di gedung Oost Java Bioscoop di Konigsplein Noord , dan 

Rapat kedua, Minggu, 28 Oktober 1928, di Gedung Oost-Java Bioscoop, membahas masalah pendidikan. Kedua pembicara, Poernomowoelan dan Sarmidi Mangoensarkoro, berpendapat bahwa anak harus mendapat pendidikan kebangsaan, harus pula ada keseimbangan antara pendidikan di sekolah dan di rumah. Anak juga harus dididik secara demokratis.

Pada rapat ketiga yaitu rapat penutup, di gedung Indonesische Clubgebouw di Jalan Kramat Raya 106, Sunario menjelaskan pentingnya nasionalisme dan demokrasi selain gerakan kepanduan. Sedangkan Ramelan mengemukakan, gerakan kepanduan tidak bisa dipisahkan dari pergerakan nasional. Gerakan kepanduan sejak dini mendidik anak-anak disiplin dan mandiri, hal-hal yang dibutuhkan dalam perjuangan.

Rapat ketiga diawali dengan kekecewaan para anggota kepanduan Indonesia, yang dilarang polisi Belanda untuk ikut hadir, karena pemuda di bawah 18 tahun dilarang mengikuti kegiatan politik. Selama sidang-sidang tersebut, para pembicara menyampaikan pendapat serta gagasannya mengenai bangsa dan negara Indonesia.

Setelah itu, dilakukan istirahat untuk merangkum dan merumuskan seluruh pendapat dan gagasan yang disampaikan selama kongres. Di waktu istirahat, W.R. Supratman , seorang wartawan yang gemar musik meminta izin kepada ketua sidang, Sugondo, untuk dapat memperdengarkan lagu gubahannya yang dinamakan “Indonesia Raya.” Karena dalam syair terdapat banyak kata “Indonesia”, Sugondo kuatir akan timbul lagi insiden dengan polisi Belanda.

Oleh karena itu ia hanya mengizinkan Supratman untuk memperdengarkan lagu Indonesia Raya dengan biolanya. Demikianlah lagu Indonesia Raya untuk pertama kali diperdengarkan dalam suatu acara resmi, yaitu dalam Kongres Pemuda II pada 28 Oktober 1928. Setelah istirahat, rapat ketiga dibuka kembali dan Sugondo sebagai ketua sidang membacakan usul resolusi sebagai berikut (Dikutip sesuai aslinya dengan ejaan lama) : 

POETOESAN CONGRES PEMOEDA-PEMOEDI INDONESIA

Kerapatan pemoeda-pemoeda Indonesia jang berdasarkan kebangsaan, dengan namanja Jong Java, Jong Soematra (Pemoeda Soematra), Pemoeda Indonesia, Sekar Roekoen, Jong Islamieten Bond, Jong Celebes, Pemoeda Kaoem Betawi dan Perhimpoenan Peladjar-Peladjar Indonesia; Memboeka rapat pada tanggal 27 dan 28 Oktober tahoen 1928 di negeri Djakarta; Sesoedahnja menimbang segala isi-isi pidato-pidato dan pembitjaraan ini; Kerapatan laloe mengambil kepoetoesan:

Pertama : KAMI POETERA DAN POETERI INDONESIA MENGAKOE BERTOEMPAH DARAH JANG SATU, TANAH INDONESIA.

Kedoea : KAMI POETERA DAN POETERI INDONESIA MENGAKOE BERBANGSA JANG SATOE, BANGSA INDONESIA

Ketiga : KAMI POETERA DAN POETERI INDONESIA MENDJOENDJOENG BAHASA PERSATUAN, BAHASA INDONESIA

Setelah mendengar poetoesan ini, kerapatan mengeloearkan kejakinan azas ini wajib dipakai oleh segala perkoempoelan kebangsaan Indonesia. Mengeloearkan kejakinan persatoean Indonesia diperkoeat dengan memperhatikan dasar persatoeannya: KEMAOEAN SEDJARAH BAHASA HOEKOEM ADAT PENDIDIKAN DAN KEPANDOEAN dan mengeloearkan pengharapan soepaja poetoesan ini disiarkan dalam segala soerat kabar dan dibatjakan di moeka rapat perkoempoelan-perkoempoelan.

Sidang menerima usulan resolusi tersebut, yang kemudian menjadi keputusan Kongres yang kini dikenal sebagai Sumpah Pemuda 28 Oktober 1928. Pada 23 April 1929, di Gedung IC di Kramat 106, diselenggarakan pertemuan antara wakil-wakil Jong Jawa,Jong Indonesia (Pemuda Indonesia) dan Jong Sumateranen Bond dan menghasilkan keputusan, untuk mendirikan suatu wadah bagi seluruh organisasi kepemudaan di India Belanda.

Disepakati pembentukan komisi persiapan yang dinamakan Komisi Besar Indonesia Muda. Wadah baru tersebut, Indonesia Muda, yang merupakan peleburan dari Jong Sumateranen Bond, Jong Celebes, Jong Jawa, Jong Indonesia dan Sekar Rukun, diresmikan dalam Kongres I tanggal 29 desember 1930 – 2 Januari 1931 di Surakarta (Solo). ***

SUMBER: http://batarahutagalung.blogspot.co.id/2006/02/renungan-28-oktober.html
http://semangatpemuda-indonesia.blogspot.co.id/p/sejarah-sumpah-pemuda.htm

Dari Permainan Silogisme ke Komputer Jamur Lendir

Dari Permainan Silogisme
ke Komputer Jamur Lendir

Armahedi Mahzar (c) 2016

Silogisme adalah molekul-molekul argumentasi logis yang ilmunya dikembangkan oleh Aristoteles ratusan tahun sebelum masehi. Leibniz menunjukkan bahwa sebenarnya hanya ada 24 bentuk silogisme yang absah. George Boole mengembangkan aljabar logika, yang kini digunakan pada perancangan komputer elektronika, untuk memecahkan persoalan silogisme dan penalaran yang lebih umum. 

Penulis buku Alice in Wonderland, Lewis Carroll, menciptakan sebuah permainan logika www.cut-the-knot.org/LewisCarroll/LCGame.shtml seperti permainan dam-daman

yang bisa digunakan sebagai alat menalar suatu silogisme yang daftarnya ada pada tulisan http://integralist.blogspot.co.id/2014/02/aritmetika-silogisme-armahedi-mahzar-c.html.

Tabel silogisme Leibniz
ungkapan verbal

Katanya, permainan ini mudah sehingga bisa diajarkan pada siswa SMP. Sedihnya, saya yang sudah lulus SMP 60 tahun yang lalu gagal paham permainan yang katanya mudah itu. -

Permainan Barang-barang -

Untungnya, setelah 15 tahun pensiun, saya akhirnya menemukan permainan barang-barang yang begitu sederhananya sehingga bisa diajarkan pada anak TK. Contohnya bisa dibaca pada http://hypernumber.blogspot.co.id/2015/09/combinatoric-logic-game-of-marbles.html .

Tabel Silogisme Leibniz
formasi kelereng kotak

Dalam permainan itu semua huruf berbeda pelambang pengertian berbeda diganti dengan kelereng dengan warna Tabel silogisme Leibnberbeda. Kalau huruf itu diawali ALL atau IS NOT, maka kelerengnya dimasukkan dalam kotak. Kalau diawali SOME atau IS maka kelerengnya ada di luar kotak.  

Nah, dengan aturan sederhana itu kita dapat menyatakan kedua alasan suatu silogisme dalam kumpulan 4 kelereng 3 warna. Kesimpulan silogisme didapat dengan membaca kumpulan 2 kelereng setelah membuang 2 kelereng sewarna beserta kotaknya. Mudah bukan? Saya pikir anak TK bisa diajari permainan susun bongkar itu.

Permainan ini bisa disederhanakan dengan cara mengganti kotak-kotak itu dengan sehelai kartu. Cara mainnya bisa dibaca di hypernumber.blogspot.com/2015/09/combinatoric-logic-game-of-anything_2.html.

 
Tabel Silogisme Leibniz
formasi kelereng kartu

Kartu bisa kita ganti dengan sehelai kertas apa saja dan kelereng berwarna bisa diganti dengan benda apa saja seperti pada https://integralisme.wordpress.com/2015/09/21/1082/.

Pernyataan kategoris
formasi barang kertas

silogisme Barbara
formasi barang kertas

Lebih sederhana lagi jika kelereng berwarna kita ganti dengan kartu berwarna, sehingga kita tak lagi memerlukan kartu penanda. Perbedaan keadaan cukup dinyatakan oleh orientasi kartu itu. Permainan itu dibahas di hypernumber.blogspot.com/2015/09/combinatoric-logic-game-of-cards.html
 

Add caption

Kartu berwarna bisa diganti dengan batang berwarna seperti pada https://integralisme.wordpress.com/2015/09/21/1082/ .

Bermain dengan Papan 

Jika dibandingkan permainan Lewis Carroll yang "susah" itu, permainan saya bukanlah permainan dengan papan bermain tetapi, pada pada hakekatnya, sebuah permainan soliter dengan kartu. Namun dia sebenarya juga bisa dilakukan di atas sebuah papan catur dan bidaknya sebagai variabel di mana posisi di kotak hitam atau putih menentukan tanda dari variabel itu.

 
Konfigurasi Catur
silogisme Barbara
K=s, Q=p, R=m

Petak-petak papan catur itu ada dua warna, tetapi petak-petak Go, permainan dari China kuno yang konon lebih sulit dari catur, hanya ada satu warna. Bagaimana pun di dalamnya ada dua posisi: dalam kotak dan pada persilangan dua garis. Jadi permainan silogisme saya juga bisa dijalankan pada papan Go dengan menggunakan batu-batu berwarna.

Konfigurasi Go
silogisme Barbara,
hitam=s, merah=m, hijau=p

Komputer Jamur Lendir

Tetapi yang menarik adalah kenyataan bahwa jamur lendir Physarum polycephalum bisa disimulasikan bertumbuh di papan Go untuk membentuk formasi-formasi silogisme Aristoteles seperti yang ditunjukkan oleh https://fedcsis.org/proceedings/2015/pliks/236.pdf . Bahkan jamur lendir dapat dibuat menjadi komponen-komponen sebuah komputer biologis yang menakjubkan http://www.wired.com/2013/06/slime-mold-computers/

Soalnya, perilaku pencarian makan Plasmodium dapat dipandang sebagai sebuah komputasi dimana data dinyatakan oleh distribusi penarik dan penolaknya di dalam ruang dan hasilnya direpresentasikan oleh struktur jaringan protoplasma. Plasmodium dapat memecahkan persoalan komputasi secara paralel. Tahun lalu di York Inggris diselenggarakan sebuah konferensi Eropa tentang berbagai aspek komputer jamur lendir itu.

 https://www.youtube.com/watch?v=czk4xgdhdY4 

Ringkasnya, makhluk-makhluk satu sel itu secara kolektif merupakan sebuah komputer cerdas analog dengan kolektivitas sel saraf yang terjaring dalam otak manusia. Tampaknya di masa depan kita harus berdamai dengan makhluk-makhluk menjijikkan itu dalam satu kerjasama komputasional tingkat tinggi.

Lagu Kebangsaan dan Mem Akustik

Lagu Kebangsaan dan Mem Akustik

Armahedi Mahzar (c) 2016 -

Pada zaman dahulu kala, ketika blog multiply.com masih hidup saya terlibat perdebatan mencerahkan dengan Dr.Tika Sukarna https://www.facebook.com/tika.sukar... dan Dr.Merlyna Lim https://www.facebook.com/merlyna.li... (waktu itu mereka masih Mahasiswa di Amerika Serikat) tentang lagu kebangsaan. Soalnya, saya memandang remeh Malaysia yang lagu kebangsaanya, Negaraku, adalah jiplakan dari lagu Terang bulan gubahan Gesang, karena begitulah pengetahuan saya waktu itu.
Tika http://www.asianscientist.com/autho... , yang SD nya di Malaysia justru membantahnya. Inti bantahannya terdapat dalam artikel Wikipedia berikut ini: - "Lagu Negaraku ( Jawi : ﻻڬﻮ ﻧڬﺎﺭﺍﮐﻮ , bahasa Tionghoa : 我的祖國 , bahasa Tamil: நெகாராகூ ) merupakan lagu resmi dari Kesultanan Perak . Lagu Terang Bulan , yang berasal dari pulau Mahé di Kepulauan Seychelles dan diadopsi oleh Raja Abdullah setelah pulang dari pengasingan di Seychelles. Iramanya berasal dari lagu "La Rosalie" digubah oleh seorang komposer berkebangsaan Perancis , Pierre Jean de Beranger (1780-1857), kemudian digubah ulang dan diberi judul "Allah Lanjutkan Usia Sultan" seterusnya dijadikan lagu resmi Kesultanan Perak ketika pertabalan raja Edward VII 1901.

 Irama lagu Negaraku ini juga sama dengan irama lagu Mamula Moon yang dipopulerkan oleh Felix Mendelssohn dan Hawaiian Serenaders. - Lagu resmi negeri Perak "Allah Lanjutkan Usia Sultan" ini dipilih menjadi lagu nasional Malaysia oleh dewan peradilan yang diketuai oleh Tunku Abdul Rahman pada 5 Agustus 1957 . Rapat pemilihan lagu kebangsaan ini berlangsung di Kantor Polisi Depoh, Kuala Lumpur . Sebanyak 4 buah lagu telah diperdengarkan oleh Korps Band Polisi Diraja Malaysia. 

Lagu Allah Lanjutkan Usia Sultan kemudian dipilih. Keputusan dewan peradilan ini kemudian disampaikan kepada Majlis Raja-raja Melayu. - Setelah disetujui, kerajaan mengeluarkan hadiah RM 1,000 kepada penggubah lagu untuk membuat liriknya. Hadiah ini dimenangkan oleh Saiful Bahri dan lirik lagu kebangsaan 'Negaraku' gubahan dia terdapat dalam 3 versi. Lagu Negaraku digubah iramanya menjadi lebih menarik oleh Mahathir Mohamad, Perdana Menteri Malaysia ke-4. Lagu Negaraku yang baru ini dinyanyikan di Dataran Merdeka tengah malam 30 Agustus 2003". (https://id.wikipedia.org/wiki/Negar...)
Merlyna http://carleton.ca/sjc/profile/lim-... justru mengejutkan saya dengan menunjukkan fakta bahwa Indonesia Raya adalah plagiasi dari lagu Jazz Belanda Lekka Lekka mengutip Remy Silado: "Menurut Remy, INDONESIA RAYA yang kita kena sebagai lagu kebangsaan kita sudah populer sejak abad ke-18 hingga tahun 1930-an. Bercorak jazz klasik, tegolong hot jazz. Judulnya: LEKKA-LEKKA atau PINDA-PINDA. 

Tetapi pada tahun 1927 lagu itu direkam dalam piringan hitam menjadi INDONEES-INDONEES. - Lantas, pada 28 Oktober 1928 dalam kongres pemuda di Jakarta diubah menjadi INDONESIA RAYA. "Penggubah lagu yang dimaksud adalah pemimpin band jazz di Makassar pada 1920. Siapa lagi kalau bukan Wage Rudolf Supratman," tulis Remy. Supratman muda memang biasa memainkan musik jazz untuk mengiringi orang Belanda berdansa-dansi. "Saban malam Minggu ia memainkan jazz bersama Kaerne." ( hurek.blogspot.com/2007/08/remy-sil... ) 

Tentu saja saya sangat sedih mengetahui hal itu, namun belakangan saya tahu pula bahwa God Save the Queen adalah lagu tradisional yang dihidupkan pada tahun 1745, Star Spangled Banner nyatanya adalah lagu To Anacreon in Heaven milik masyarakat pemabuk Inggris, Marseilles adalah tiruan karya yang digubah oleh Giovan Battista Viotti pada tahun 1781 – 11 tahun sebelum Claude Joseph Rouget de Lisle menulis lagu kebangsaan Prancis itu, dan banyak lagi lagu kebangsaan lain sebenarnya lagu jiplakan juga ( www.bbc.com/news/magazine-34052000 dan https://republicordeath.wordpress.com/2015/08/28/national-plagiarism-2-plagiat-national/ ). 

Maka, saya pun tak sedih lagi, bahkan tercerahkan: melodi adalah mem akustik yang sangat kuat sebelum adanya mem digital di internet. :) :) :) Begitu kuatnya mem akustik itu sehingga para komponis terkenal lagu-lagu klasik pun tak bisa menghindar dari virus mental ini. Mozart , misalnya, menggubah The Beneficent Dervish menjiplak The Magic Flute—Dschinnistan, karya Christoph Martin Wieland. http://www.slate.com/articles/arts/...

Beethoven

  menggunakan Canon gubahan Pachelbel dalam rondo pada Piano Sonata Op. 28 ( http://www.slate.com/articles/arts/... ). Dia bahkan menjiplak karya Mozart “Misericordias Domini,” K. 222, memodifikasinya menjadi “Ode to Joy” di bagian akhir Simfoninya yang kesembilan (http://www.theimaginativeconservative.org/... ). Juga Richard Strauss   dalam operanya Elektra mengambil 50 tema dalam opera Cassandra karya Vittorio Gnecchi.