Saya, Logika dan Internet 3

Saya, Logika dan Internet
Bagian Tiga

Armahedi Mahzar (c) 2013

Melanjutkan kisah perjalanan saya di dunia logika dengan wahana mayantara.

Pada blog yang lalu saya bercerita bahwa semua itu bermula dari pertemuan saya di mayantara dengan aljabar Brown

dari dalam buku Laws of Form yang samar itu.

Di mayantara itu juga saya menemukan aljabar Kotak Kauffman yang mengganti SILANG dalam aljabar Brown dengan KOTAK. Dalam notasi kotak itu, kedua aksioma aljabar Brown adalah

+----+

|+-+ |

||p|p| =

|+-+ |

+----+  

+---------+   +-------+

|+--+ +--+|   |+-+ +-+|

||pr| |qr|| = ||p| |q|| r

|+--+ +--+|   |+-+ +-+|

+---------+   +-------+

Ketika saya mengganti huruf-huruf di aljabar kotak Kauffman dengan bola-bola warna-warni




, 
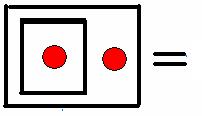
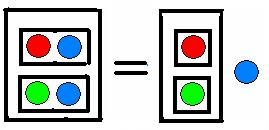maka sampailah saya pada sebuah permainan hapus-hapusan kotak warna yang isomorfik dengan aljabar logika Boole. Yang tak saya duga adalah kenyataan bahwa dengan permainan hapus-hapusan kotak warna yang kekanak-kanakan itulah saya bisa menemukan sejumlah fakta logika yang sebelumnya belum pernah ditemukan orang.

PENEMUAN PERTAMA:
aksioma REDUCTIO AD ABSURDUM

Logika Brown yang isomorfik dengan aljabar Boole itu ternyata disederhanakan menjadi aljabar Kauffman dengan satu aksioma saja, yaitu aksioma Huntington [[a][b]][[a]b]=a yang dalam notasi aljabar kotak adalah

Sebenarnya, tak ada yang original dari penemuan Kauffman ini. Soalnya, Huntington jauh-jauh hari telah menemukan bahwa aljabar Boole dapat diturunkan dari ketiga aksiomanya yaitu Komutativitas, Asosiativitas dan aksioma yang dijadikan aksioma tunggal oleh Kauffman itu. Kauffman bisa menghilangkan kedua aksioma Huntington yang lain karena penggunaan notasi kotak berdimensi dua itu komutativitas dan asosiativitas merupakan kenyataan visual yang tak perlu dinyatakan secara simbolik.

Namun, apakah sebenarnya aksioma Huntington itu? Setelah saya amati dengan cermat, jika kita menafsirkan

   pendampingan dua gambar sebagai operasi DAN dan

   menafsirkan KOSONG sebagai BENAR,

maka rumus Huntington itu tak lain dari rumus Boole

(a'->b')(a'->b) = a

bagi sebuah prinsip logika yang sangat kuno, mendahului Aristoteles, yang dikenal sebagai prinsip REDUCTIO AD ABSURDUM.

Prinsip REDUCTIO AD ABSURDUM mengatakan bahwa

  sebuah pernyataan itu benar

 jika dan hanya jika

 penyangkalannya menyimpulkan suatu yang kontradiktif atau SALAH.

Melihat hal itu tentu saja mencengangkan saya: ternyata logika modern yang matematis itu landasan terdasarnya adalah prinsip kuno yang mendahului logika tradisional Aristoteles.

PENEMUAN KEDUA:
PEMBUKTIAN KONJEKTUR ROBBINS

Penemuan lain yang menakjubkan saya adalah kenyataan bahwa dengan aljabar kotak kita bisa membuktikan aksioma Robbins dengan sangat singkat. Robbins, mahasiswa Huntington, menyatakan bahwa aksioma Huntington itu sebaiknya diganti dengan rumus Boolean yang lebih sederhana yang kemudian disebut sebagai rumus Robbins.

[[a[b]][ab]] = a

Tetapi sayangnya, Robbins tidak bisa membuktikan bahwa memang seluruh aljabar Boole bisa diturunkan dari rumusnya beserta aksioma komutasi dan aksioma asosiasi. Berpuluh tahun matematikawan mencoba membuktikan kebenaran konjektur atau dugaan Robbins itu, namun gagal semua. Baru pada awal milenium ketiga ini William Mccune dengan bantuan program komputer ... bisa membuktikannya dengan menggunakan waktu mesin komputer selama lima hari.

Kauffman sendiri dengan menggunakan aljabar kotak bisa mereduksi pembuktian komputer yang sangat panjang itu menjadi pembuktian 14 buah lemma atau dalil bantu.

Saya tidak menyangka bahwa saya, menggunakan aljabar kotak, bisa menurunkan aksioma Huntington dari rumus Robbins dengan menggunakan sifat dualitas aljabar Boole hanya dalam  3 langkah.

[[a[b]][ab]]=a

Langkah 1: negasikan kedua ruas x=y -> [x]=[y]

[[[a[b]][ab]]]=[a]

Langkah 2: hapus negasi ganda karena [[x]]=x

  [a[b]][ab]  =[a]

Langkah 3: ganti [a] dengan A, sebaliknya a dengan [A] dan b dengan B

[[A][B]][[A]B]= A

yang tak lain dari pada Aksioma Huntington itu sendiri

Ajaib. Namun sebenarnya saya telah menggunakan dua identitas Boole yang belum dibuktikan sebagai kaidah inferensi.Bagi banyak orang ini mungkin sebuah penyelundupan yang ilegal, namun bagi saya ini bukannya sebuah kesalahan, tetapi keunggulan manusia untuk memilih kaidah inferensi yang tepat. Misalnya Charles Sanders Peirce mempunyai lima kaidah inferensi fundamental..

Bagaimana pun, yang lebih mengherankan saya adalah kenyataan bahwa aksioma Robbins itu pun tak lain tak bukan daripada prinsip REDUCTIO AD ABSURDUM juga jika rumusnya dibaca dengan penafsiran Brown tentang aljabar kotak, dimana

  pendampingan dibaca sebagai ATAU dan

  KOSONG dibaca sebagai SALAH.

Bagi saya penemuan ini memperkuat ketercengangan saya ketika mengetahui bahwa prinsip REDUCTIO AD ABSURDUM adalah fondasi aljabar logika modern Boole.

PENEMUAN KETIGA:
KESATUAN SEMUA SILOGISME

Dengan bermain kotak logika berwarna ini, akhirnya saya menemukan bahwa semua silogisme absah Aristoteles Leibnitz itu, sebenarnya, adalah satu adanya. Asalnya, saya membaca di internet bahwa Christine Ladd-Franklin menemukan satu rumus antilogisme yang bisa menurunkan semua silogisme absah yang menurut Leibnitz ada 24. Untuk membuktikan kebenaran dalil Ladd-Franklin itu saya mengubah formula antilogisme itu dalam gambar aljabar kotak yang dengan aturan hapus-hapusan menghasilkan satu kotak kosong. Ini artinya kedua alasan satu silogisme jika digabungkan dengan penyangkalan kesimpulannya adalah kontradiktif alas SALAH.

Sayangnya pada mulanya saya hanya menemukan dua buah antilogisme 

     Ebc Aab Iac

     Abc Aab Oac

yang bisa menurunkan hanya 15 buah silogisme absah.

Namun belakangan saya dapat menemukan dua lagi antilogisme yaitu

     Eaa Ebc Aab Aac
     Ebb Abc Aab Eac

yang bisa menurunkan 9 buah silogisme sisanya.

Untunglah, pada akhirnya saya bisa membuktikan bahwa keempat antilogisme itu ekivalen satu sama lainnya.

Dengan demikian dalil Ladd-Franklin itu terbukti kebenarannya.

Namun, sebagai dampak sampingan, justru ada dalil lebih umum yang saya temukan:

    semua silogisme itu ekivalen satu sama lainnya.

Jadi setiap silogisme absah sebenarnya, bukan hanya bisa diturunkan bukan hanya dari sebuah antilogisme, tetapi dari silogisme absah yang mana pun.

PENEMUAN KEEMPAT:
SISTEM GRAF EKSISTENSIAL SEDERHANA

Namun perjalanan selanjutnya di Internet, saya menemukan suatu sistem logika simbolik yang lebih sederhana dari aljabar Brown yaitu sistem graf eksistensial dari Charles Sanders Peirce yang hanya mengenal aksioma tunggal yaitu KOSONG. Namun sayangnya sistem Peirce itu memerlukan lima kaidah inferensi.

Jadi sistem Graf Eksistensial Peirce terdiri dari

satu aksioma

   kebenaran   : KOSONG

dan lima kaidah inferensi

   Delesi      : pq -> p 

   Insersi     : [p] -> [pq]

   Iterasi     : p[q] -> p[pq]

   Deiterasi   : p[pq] -> p[q]

   Negasi ganda: [[p]] = p

Rupanya Peirce menyembunyikan rumus-rumus implikatif Boole ke dalam kaidah-kaidah inferensi.

Tentu saja, saya agak kecewa melihat kenyataan ini. Namun, alhamdulillah, saya akhirnya menemukan bahwa kita dapat mermbuang empat kaidah inferensi itu menjadi satu saja yaitu ITERASI p[q]->p[pq], jika saja kita mau mengganti aksioma tunggal Peirce itu dengan sebuah aksioma baru yaitu KONSISTENSI p->p.

Dengan demikian seluruh aljabar Boole dapat diturunkan dari sistem graf eksistensial sederhana

M0 aksioma KONSISTENSI:   p -> p

M1 Kaidah  ITERASI    : p[q]= p[pq]

Tentu saja penemuan ini sangat membahagiakan saya. Soalnya, pada akhirnya saya menemukan bahwa semua isi alam logika sebenarnya berdasarkan satu asas saja yaitu konsistensi.

Setelah saya perhatikan dengan teliti ternyata bahwa aksioma konsistensi p->p bagi sistem graf eksistensial sebenarnya dapat diganti dengan dengan aksioma yang lebih sederhana yaitu INDIFERENSI  p->BENAR atau [p[ ]] . Dengan demikian sistem graf eksistensial yang paling sederhana adalah

M0 aksioma INDIFERENSI:     p -> 1 

M1 kaidah ITERASI     :  p[q] = p[pq].

CATATAN AKHIR

Kalau diperhatikan keempat penemuan itu sebenarnya sebuah perjalanan menuju proses penyederhanaan sistem aksiomatika logika. Ini adalah dimensi abstrak perjalanan logika saya. Sisi lain perjalanan saya yang lain adalah perjalanan menuju penyederhanaan notasi logika dari yang literal menuju yang obyektif konkret, dari aljabar logika abstrak menuju permainan logika kongkret. Bagaimana hasil pencarian saya akan permainan logika tersederhana itulah yang akan saya ceritakan pada blog lainnya lagi.